Una breve historia sobre las aportaciones de Isaac Newton y Leibniz al calculo diferencial .
Los grandes creadores del Cálculo diferencial fueron el inglés Isaac Newton (1642--1727) y el alemán Gottfried Wilhelm Leibniz (1646--1716).
De manera diferente pero independientemente estos grandes intelectuales de los siglos XVII y XVIII sistematizaron y generalizaron ideas y procedimientos que habían sido abordados (de diferentes maneras) y con éxito parcial desde la Antigüedad.
De manera diferente pero independientemente estos grandes intelectuales de los siglos XVII y XVIII sistematizaron y generalizaron ideas y procedimientos que habían sido abordados (de diferentes maneras) y con éxito parcial desde la Antigüedad.
Antes de Newton y Leibniz fueron realizados diversos aportes de importancia asociados al nombre de grandes personalidades, como por ejemplo: Gilles de Roberval (1602--1675), Johannes Kepler (1571--1630), René Descartes (1596--1650), Pierre de Fermat (1601--1665), Galileo Galilei (1564--1642), Christian Huygens (1629--1695, amigo de Leibniz), John Wallis (1616--1703, amigo de Newton), Bon aventura Cavalieri (1598--1647, discípulo de Galileo), Evangelista Torricelli (1608--1647, discípulo de Galileo), Isaac Barrow (1630--1677, maestro de Newton).
Para tener la perspectiva científica e histórica apropiada, debe decirse que una de las contribuciones previas decisivas para el trabajo de Newton y Leibniz fue la Geometría Analítica (la expresión de puntos geométricos en coordenadas y el uso de métodos algebraicos), creado independientemente por Descartes y Fermat.
Biografías.
Isaac Newton.
Isaac Newton (25 de diciembre de 1642 JU – 20 de marzo de 1727 JU (4 de enero de GR – 31 de marzo de 1727 GR) fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de los Philosophiae naturalis principia mathematica, más conocidos como los Principia, donde describió la ley de gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre.
Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks) y el desarrollo del cálculo matemático.
Investigaciones de Isaac Newton.
Desde finales de 1664 trabajó intensamente en diferentes problemas matemáticos.
Abordó entonces el teorema del binomio.
Teorema generalizado del binomio (Newton)
Isaac Newton generalizó la fórmula para tomar otros exponentes, considerando una serie infinita:
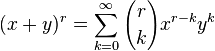
Donde r puede ser cualquier número complejo (en particular, r puede ser cualquier número real, no necesariamente positivo ni entero), y los coeficientes están dados por:
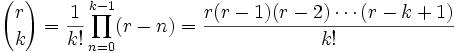
En 1669 su mentor, Isaac Barrow, renunció a su Cátedra Lucasiana de matemática, puesto en el que Newton le sucedería hasta 1696.
El mismo año envió a Luis Zeus, por medio de Barrow, su "Analysis per aequationes número terminorum infinitos".
Para Newton, este manuscrito representa la introducción a un potente método general, que desarrollaría más tarde: su cálculo diferencial e integral.
Newton había descubierto los principios de su cálculo diferencial e integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.
Newton y Leibniz protagonizaron una agria polémica sobre la autoria del desarrollo de esta rama de la matemática.
Newton había descubierto los principios de su cálculo diferencial e integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.
Newton y Leibniz protagonizaron una agria polémica sobre la autoria del desarrollo de esta rama de la matemática.
Los historiadores de la ciencia consideran que ambos desarrollaron el cálculo independientemente, si bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba mejor a problemas prácticos.
La polémica dividió aún más a los matemáticos británicos y continentales, sin embargo esta separación no fue tan profunda como para que Newton y Leibniz dejaran de intercambiar resultados.
Newton abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones.
Newton abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones.
Newton también buscaba cómo cuadrar distintas curvas, y la relación entre la cuadratura y la teoría de tangentes.
Después de los estudios de Roberval, Newton se percató de que el método de tangentes podía utilizarse para obtener las velocidades instantáneas de una trayectoria conocida.
En sus primeras investigaciones Newton lidia únicamente con problemas geométricos, como encontrar tangentes, curvaturas y áreas utilizando como base matemática la geometría analítica de Descartes.
No obstante, con el afán de separar su teoría de la de Descartes, comenzó a trabajar únicamente con las ecuaciones y sus variables sin necesidad de recurrir al sistema cartesiano.
Leibniz.
Nació el 1 de julio de 1646 en Leizpig, (Alemania). Hijo de un profesor de filosofía.
Cursó estudios en universidades de su ciudad con apenas quince años, donde se conoce el pensamiento aristotélico, platónico y escolástico, así como con la filosofía de Descartes, posteriormente los continuaría en Jena y Altdorf. En 1666 fue premiado con un doctorado en leyes, además de trabajar para Johann Philipp von Schönborn, arzobispo elector de Maguncia. Declinó la oferta de dedicarse a la enseñanza en la universidad y orientó su vida a la carrera política y diplomática.
En 1673 se trasladó a París, donde pasó tres años y además visitó Amsterdam y Londres, donde se dedicó al estudio de las matemáticas, la ciencia y la filosofía. En 1676 traba como bibliotecario y consejero privado en la corte de Hannover y hasta la fecha de su fallecimiento estuvo al servicio de Ernesto Augusto,duque de Brunswick-Lüneburg, más tarde elector de Hannover, y de Jorge Luis, elector de Hannover, después Jorge l, rey de Gran Bretaña.
Investigaciones de Leibniz.
Las contribuciones de Leibniz en el campo del cálculo infinitesimal, efectuadas con independencia de los trabajos de Newton, así como en el ámbito del análisis combinatorio, fueron de enorme valor. Introdujo la notación actualmente utilizada en el cálculo diferencial e integral.
Los trabajos que inició en su juventud, la búsqueda de un lenguaje perfecto que reformara toda la ciencia y permitiese convertir la lógica en un cálculo, acabaron por desempeñar un papel decisivo en la fundación de la moderna lógica simbólica.
Sin duda Leibniz merece igual crédito que Newton, por lo tanto sus aportaciones al cálculo fueron sobresalientes. Leibniz estableció la resolución de los problemas para los máximos y los mínimos, así como de las tangentes, esto dentro del cálculo diferencial; dentro del cálculo integral logró la resolución del problema para hallar la curva cuya subtangente es constante.
Aportaciones de Leibniz al calculo diferencial.
Leibniz estableció la resolución de los problemas para los máximos y los mínimos, así como de las tangentes, esto dentro del cálculo diferencial; dentro del cálculo integral logró la resolución del problema para hallar la curva cuya subtangente es constante.
Expuso los principios del cálculo infinitesimal, resolviendo el problema de la isócrona (ver biografía de Bernoulli) y de algunas otras aplicaciones mecánicas, utilizando ecuaciones diferenciales.
No cabe duda que su mayor aportación fue el nombre de cálculo diferencial e integral, así como la invención de símbolos matemáticos para la mejor explicación del cálculo, como el signo = (igual), así como su notación para las derivadas dx/dy, y su notación para las integrales.
Conflicto.
Cada uno trabajo en otros campos diferentes a las matemáticas.
Newton es un conocido científico que hizo grandes descubrimientos en los campos de física y matemáticas.
Por otra parte Leibniz destaco en las matemáticas y la filosofía.
Los dos son personajes destacados en la historia de las matemáticas, ahora nos centraremos en explicar los antecedentes que condujeron al conflicto que mantuvieron por defender la autoria de la invencion y desarrollo del calculo.
Newton empezó a desarrollar su calculo diferencial hacia el 1665, dio un enfoque geométrico y analítico a las derivadas.
Su principal aplicación era para calcular tangentes, curvaturas y áreas.
Para Newton un fluente x era la cantidad de movimiento continuo de un punto que traza
una curva y una fluxión x_ su velocidad.
El problema se basa en hallar la relacion entre las fluxiones (valores) dadas una relacion de fluentes.
Se trataba de un conjunto de reglas para poder calcular máximos, mínimos
y tangentes.
El mismo Newton reconoció que su interpretación era algo dificultosa y la perfecciono en trabajos posteriores.
Newton no solía publicar sus trabajos inmediatamente.
De hecho su investigación sobre las derivadas las escribió en un tratado informal, De
Analysi en 1669, que compartió con sus compañeros del ˜ Trinity College.
Este manuscrito contenía una introducción al calculo diferencial e integral que desarrollo mas tarde.
No se llego a publicar, en una obra propia de Newton, hasta después de su muerte en De Methodis Serierumet Fluxionum escrito en 1671 y publicado en 1673.
El propio Newton escribió dos cartas enunciando sus descubrimientos para que fueran remitidas a Leibniz. Newton desarrollo y perfecciono la serie del binomio hacia el a ´ no 1664. En particular se podía usar para exponentes que sean fracciones o números negativos, por lo que una aplicación practica era el calculo de raíces cuadradas.
Las cartas, que detallaban este método y citaban algunos ejemplos, las mando a la Royal Society of London para que se encargaran de hacerlas llegar a Leibniz.
Mientras tanto Leibniz también habia estado trabajando en esta materia pero de forma independiente a Newton.
Leibniz trabajaba con sumas de sucesiones para aproximar la cuadratura de una curva, de forma que cuanto mas peque ´ na fuera la distancia entre dos números de la sucesión mejor apreciación seria a la curva.
De esta manera también se aproxima la tangente como la diferencia entre dos puntos.
Por tanto Leibniz observa que la integracion y la derivacion son operaciones inversas.
Leibniz fue desarrollando su notación hasta encontrar una que le ´
permitiera trabajar mas intuitivamente.
Leibniz consideraba una curva como infinitas porciones de recta donde dx es la diferencia infinitesimal de dos puntos consecutivos del eje de abscisas.
Por tanto R y dx es la suma de rectángulos infinitesimales y dx, el símbolo R
es la alargacion de una S que significa suma.
Esta notación es la que aun usamos en la actualidad.
Comparacion.
Newton consideraba las variables en funcion del tiempo, en cambio Leibniz tenia un enfoque diferente.
El pensaba que las varaibles tomaban secuencias de valores infinitamente cercanos, de aqui las notaciones dx y dy (donde x , y son variables) que representan las diferencias entre
valores consecutivos de las secuencias.
Tambien dedujo que el cociente dx/dy da la tangente.
Sobre la integracion, para Newton se basaba en encontrar la relacion entre lo que denomina fluxiones, es decir, las derivadas.
De esta forma implica que la integracion es la operacion inversa a la derivacion.
Leibniz usa la integral como una suma de infinitesimales, en cambio Newton usaba velocidades finitas.
Aunque ninguno de los dos usaba las funciones tal como se usan actualmente, mas bien pensaban en terminos de gráficas.
Conclusion.
A pesar de que el conflicto tenia como finalidad dar la autoria de la invencion del Calculo a uno de los dos, y el reconocimiento que eso conlleva, la verdad es que ambos acabaron mal parados.
Ambos habian cometido errores: Newton, al no publicar formalmente sus descubrimientos, y
Leibniz, al no mencionar que habia tenido contacto con el trabajo de Newton y no compartir la autoria del descubrimiento.
¿Este conflicto se pudo haber evitado? Según algunas hipótesis la guerra anglo-alemana que hubo nunca debería haber comenzado, y mucho debería haberse desarrollado como se desarrollo.
Aunque ambos pusieron las bases del Calculo de manera independiente, ni mucho menos fueron los primeros en dar las nociones iniciales de esta rama matematica.
El precursor de estas ideas fue Pierre de Fermat.
Leibniz reconocía en una carta a Wallis, un matemático ingles, que le debía mucho a Fermat; y Newton escribió que desarrollo su calculo diferencial en base al método de trazar tangentes de Fermat, que trataba exactamente los máximos y mínimos de curvas polinomicas.
Actualmente, toda la comunidad científica reconoce a ambos como los descubridores del calculo, y se sigue utilizando la notación de ambos, con diferencias entre matemáticas y física.
En física, se utiliza la notación de Newton para la diferenciación, la cual consiste en un punto sobre el nombre de la funcion, y que Newton denomino fluxión.
Es muy utilizada para la derivada respecto del tiempo.
En la notación de Leibniz se representa la operacion de diferenciar mediante el operador d/dx.
Esta notación permite recordar intuitivamente varios conceptos del calculo como la regla de la cadena, o el de separación de variables en la resolución de ecuaciones diferenciales.
La notación de Leibniz resulta muy útil cuando se trabaja con derivadas parciales de funciones multivariables y sus operadores derivados, ya que indica que variable de la funcion es independiente en cada momento.
En el siguiente enlace podrán ver algo mas sobre Newton y Leibniz.
Esto es todo por mi parte y muchas gracias, no olviden comentar.



No hay comentarios:
Publicar un comentario